首页 请复制到word或wps中编辑使用(ctrl+c,ctrl+v),vip用户页面底部可看到答案解析 公式上下对齐方法复制内容

必修一-第1章-集合

一.填空题 (共 8 小题)

1 . 设S，T是R的两个非空子集，如果存在一个从S到T的函数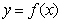满足：
(i)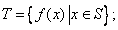(ii)对任意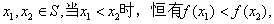
那么称这两个集合“保序同构”，现给出以下3对集合：
①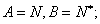
②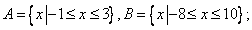
③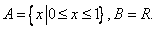
其中，“保序同构”的集合对的序号是_______。(写出“保序同构”的集合对的序号)。

2 . 设A是整数集的一个非空子集，对于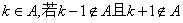，则k是A的一个“孤立元”，给定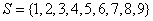，由S的3个元素构成的所有集合中，不含“孤立元”的集合共有     个。

3 . 在平面直角坐标系中，定义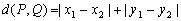为两点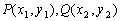之间的“折线距离”，在这个定义下，给出下列命题：
①到原点的“折线距离”等于1 的点的集合是一个正方形；
②到原点的“折线距离”等于1 的点的集合是一个圆；
③到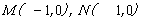两点的“折线距离”之和为4的点的集合是面积为6的六边形；
④到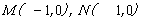两点的“折线距离”差的绝对值为1的点的集合是两条平行线；
其中正确的命题是                。(写出所有正确命题的序号)

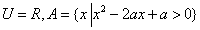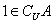4 . 集合,如果,那么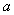的取值范围是_____.

5 . 已知集合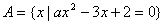至多有一个元素，则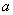的取值范围        ；
若至少有一个元素，则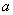的取值范围         。

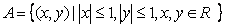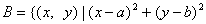
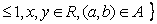6 . 已知集合,,则集合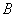所表示图形的面积是

7 . 对于平面上的点集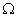，如果连接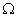中任意两点的线段必定包含于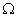，则称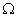为平面上的凸集，给出平面上4个点集的图形如右(阴影区域及其边界)，其中为凸集的是
         (写出其中所有凸集相应图形的序号)。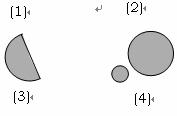

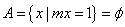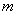8 . 已知集合，则的值为        ．　

答案和解析(vip用户才显示)